Unveiling the Unknowns: What Are the Three Undefined Geometry Terms?
Have you ever pondered the fundamental building blocks of geometry? It's a fascinating world of shapes, sizes, and spatial relationships, built upon a foundation of seemingly simple concepts. Yet, at the heart of this structured world lie three undefined terms: point, line, and plane. These terms are not merely abstract ideas; they are the bedrock upon which all geometric structures are built. Intriguingly, we describe them, not by strict definitions, but by their characteristics and the relationships they hold with each other.
Imagine trying to describe a magnificent skyscraper without mentioning its foundation. It would be near impossible! Similarly, trying to comprehend geometry without understanding the undefined terms of point, line, and plane would be like navigating a labyrinth in the dark. These terms are the invisible pillars that support all other geometric concepts, giving rise to angles, shapes, and the very space we inhabit.
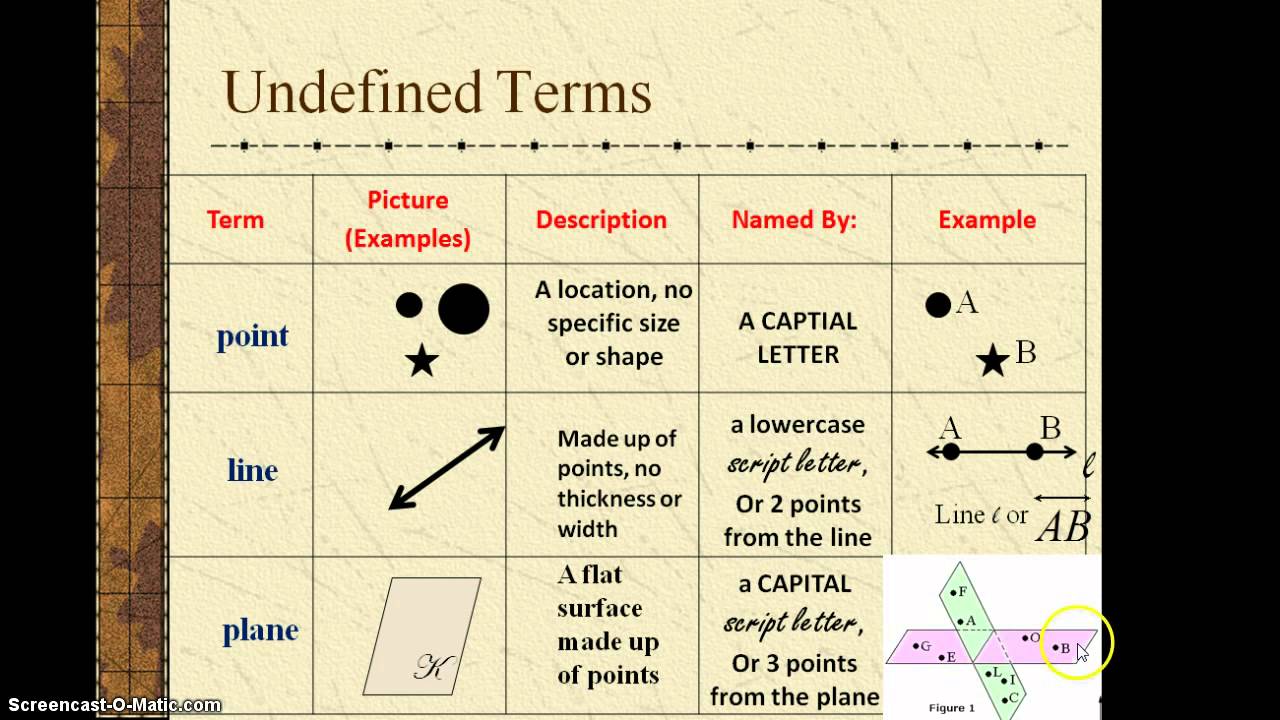
The intriguing thing about these undefined terms is their inherent simplicity. A point, represented by a dot, denotes a location in space. It has no size or dimension, yet it holds the potential for infinite possibilities. A line, on the other hand, is an infinite collection of points extending in opposite directions without end. It possesses length but lacks width and height. Then we have the plane, a flat surface extending infinitely in all directions. It has length and width but no thickness. These seemingly simple concepts, individually, might seem trivial, yet when combined, they form the very fabric of geometric reasoning.
The history of these undefined terms takes us back to ancient civilizations, where mathematicians grappled with understanding the world around them. The Greeks, in particular, are credited with formalizing these concepts in Euclidean geometry, a system that has stood the test of time. Euclid, in his renowned work, "Elements," laid the groundwork for geometry as we know it, emphasizing the importance of these undefined terms as the starting point for all subsequent definitions and theorems.
The significance of understanding these terms lies in their power to unlock the secrets of geometry. By comprehending their properties and interrelationships, we gain the tools to analyze shapes, solve spatial problems, and make sense of the world around us. From architecture to engineering, from art to technology, the applications of these fundamental concepts are boundless.
While we can't define these terms in the traditional sense, we can illustrate them with examples. Think of a star in the night sky as a representation of a point. The horizon, where the sky seems to meet the earth, can be visualized as a line. And the surface of a calm lake provides a tangible image of a plane. These everyday examples help us grasp the essence of these fundamental geometric concepts.
Advantages and Disadvantages of Working with Undefined Terms
| Advantages | Disadvantages |
|---|---|
| Provide a foundation for defining all other geometric terms. | Can be abstract and challenging to grasp initially. |
| Allow for a consistent and logical development of geometric principles. | May lead to circular reasoning if not handled carefully. |
| Promote abstract thinking and spatial reasoning skills. |
Understanding these undefined terms, the building blocks of geometry, opens a door to a world of possibilities. By grasping their essence, we equip ourselves with the tools to analyze, create, and navigate the spatial world around us. So, the next time you encounter a geometry problem, remember the fundamental trio: point, line, and plane. They are the silent heroes, the unsung foundation upon which the grand edifice of geometry rests.
The thrill of the unknown why qual o placar do jogo de hoje is more than just a score
The wonder of animal coloring pages a journey into creativity and learning
Unlocking wordle secrets your guide to wordle hint podcasts