Unlocking the Secrets of Phasor Diagrams: A Visual Symphony of Electrical Circuits
Imagine trying to orchestrate a symphony of electrical currents and voltages, each fluctuating with time, their interactions a complex dance of energy. How can we possibly grasp the intricate relationships between these oscillating quantities? Enter the elegant tool of the phasor diagram, a visual language that transforms this complex choreography into a static, comprehensible picture.
Phasor diagrams are graphical representations of alternating current (AC) circuits, providing a powerful way to visualize the magnitude and phase relationships between sinusoidal waveforms. They effectively freeze time, allowing us to analyze the steady-state behavior of AC circuits without the complexity of constantly changing values. Think of it as capturing the essence of the wave, its fingerprint, rather than tracking its every undulation.
The concept of representing sinusoidal functions with rotating vectors originated from the need to simplify AC circuit calculations. Early electrical engineers grappled with the intricacies of differential equations to describe AC phenomena. Phasor diagrams emerged as a more intuitive approach, transforming differential equations into algebraic ones, making analysis significantly simpler. Charles Proteus Steinmetz, a pioneer in electrical engineering, played a key role in popularizing the use of phasors in the late 19th and early 20th centuries, solidifying their place as an indispensable tool in electrical engineering.
The core issue addressed by phasor diagrams is the challenge of handling the phase difference between voltage and current in AC circuits. Unlike DC circuits, where voltage and current are typically in phase, AC circuits often introduce phase shifts due to the presence of reactive components like inductors and capacitors. Phasor diagrams provide a clear visual representation of these phase relationships, allowing engineers to quickly determine the overall circuit behavior.
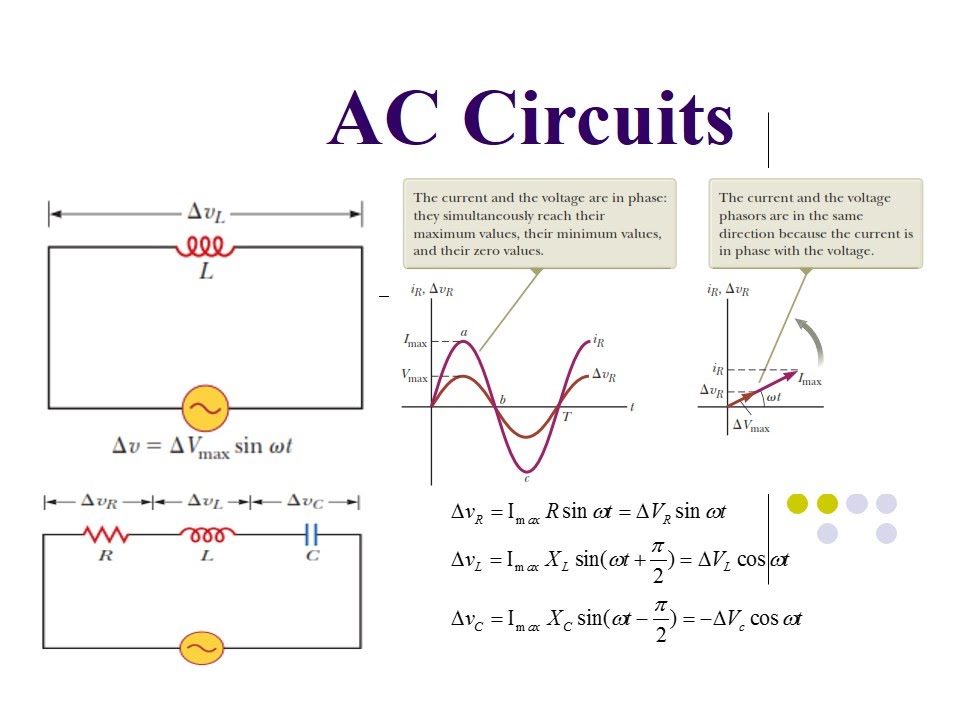
A phasor is a rotating vector whose length represents the magnitude of a sinusoidal quantity (voltage or current) and whose angle represents its phase relative to a reference. By drawing the phasors for different circuit elements on a single diagram, we can visualize their relative phase angles and use simple geometry and trigonometry to analyze the circuit.
One of the primary benefits of using phasor diagrams is their ability to simplify AC circuit calculations. By converting sinusoidal quantities into phasors, we can perform algebraic operations instead of more complex calculus. This greatly reduces the computational burden, especially in circuits with multiple components.
Another benefit lies in the visualization of phase relationships. Phasor diagrams clearly illustrate the leading or lagging relationship between voltage and current, which is crucial for understanding the power factor and resonance in AC circuits.
Finally, phasor diagrams provide a clear understanding of circuit behavior. They enable engineers to visualize the interplay of different circuit elements and predict the overall response of the circuit to different input signals.
To create a phasor diagram, represent each sinusoidal voltage or current as a rotating vector. The length of the vector is the amplitude, and the angle is the phase. Place these vectors on a coordinate system, and their relationships become immediately visible.
Advantages and Disadvantages of Phasor Diagrams
| Advantages | Disadvantages |
|---|---|
| Simplifies AC circuit analysis | Only applicable to sinusoidal waveforms |
| Visualizes phase relationships | Doesn't represent transient behavior |
| Facilitates understanding of circuit behavior | Can become complex for very large circuits |
Best Practices:
1. Clearly label all phasors.
2. Use a consistent scale for magnitude.
3. Indicate the reference phasor.
4. Use different colors or line styles for different quantities.
5. Double-check your calculations and diagram for accuracy.
FAQ:
1. What is a phasor? A phasor is a rotating vector representing a sinusoidal quantity.
2. Why are phasor diagrams used? They simplify AC circuit analysis.
3. What is the significance of the phase angle? It shows the timing relationship between sinusoidal quantities.
4. How are phasor diagrams constructed? By representing sinusoidal quantities as rotating vectors.
5. What are the limitations of phasor diagrams? They only apply to sinusoidal waveforms and steady-state conditions.
6. How can I learn more about phasor diagrams? Numerous textbooks and online resources cover this topic.
7. What software can be used to draw phasor diagrams? Several electrical engineering software packages can generate phasor diagrams.
8. What are some real-world applications of phasor diagrams? They are used in the analysis and design of power systems, motors, and other electrical devices.
In conclusion, phasor diagrams are an invaluable tool for anyone working with AC circuits. They offer a powerful visual language to understand the interplay of sinusoidal waveforms, simplifying complex analysis and offering insightful visualizations of circuit behavior. By mastering this technique, you unlock a deeper understanding of electrical engineering principles and gain the ability to tackle intricate circuit problems with greater clarity and efficiency. Embracing phasor diagram analysis is a vital step in any electrical engineer's journey, providing a powerful lens through which to view the dynamic world of AC circuits.
Unlocking savings your guide to the iga springfield ky weekly ad
Unlocking your discord tribe the ultimate guide to a killer pfp
Unlocking the secrets of your ford fusions wheel hardware
