Unit 6 Similar Triangles
Unit 6 Similar Triangles
Are you ready to dive into the fascinating world of unit 6 similar triangles? This topic may sound daunting at first, but with the right guidance, you'll soon discover the beauty and symmetry behind these geometric shapes.
Similar triangles have played a crucial role in mathematics for centuries, dating back to ancient civilizations such as the Egyptians and Greeks. The concept of unit 6 similar triangles is essential for understanding proportions, ratios, and solving complex problems in geometry.
Definition, explanation, and simple examples
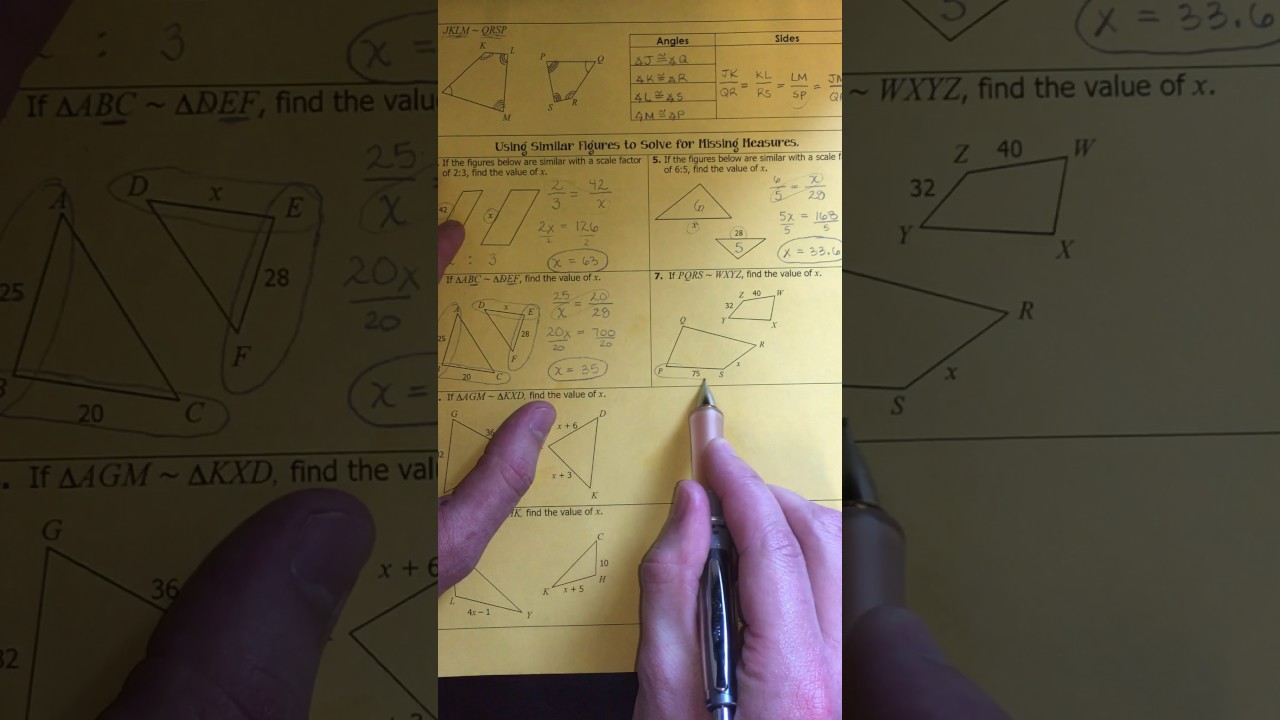
Similar triangles are polygons with the same shape but different sizes. In unit 6 similar triangles, the ratio of corresponding sides is constant, allowing us to solve for unknown lengths or angles. For example, if two triangles have angles measuring 30, 60, and 90 degrees, they are similar because the ratios of their sides are equal.
Benefits of unit 6 similar triangles
One of the main benefits of understanding similar triangles is the ability to solve real-world problems involving proportions. For instance, architects use the concept of unit 6 similar triangles to scale down large structures for building models. This ensures accuracy and efficiency in construction projects.
Action plan for unit 6 similar triangles
To master unit 6 similar triangles, start by identifying the corresponding sides and angles of two triangles. Then, apply the properties of similar triangles to set up proportions and solve for unknown variables. Practice with different examples to strengthen your understanding of this concept.
Checklist for unit 6 similar triangles
- Identify corresponding sides and angles of similar triangles
- Set up proportions using the properties of similar triangles
- Solve for unknown variables by cross-multiplying
Step-by-step guide on unit 6 similar triangles
- Identify similar triangles based on corresponding angles
- Determine the scale factor between the two triangles
- Set up proportions using the corresponding sides
- Solve for unknown lengths or angles using cross-multiplication
Recommendations for unit 6 similar triangles
For additional practice and resources on unit 6 similar triangles, check out online math platforms such as Khan Academy or textbooks like "Geometry: Concepts and Skills." These resources offer a range of examples and exercises to help you sharpen your skills in geometry.
Advantages and disadvantages of unit 6 similar triangles
One advantage of unit 6 similar triangles is their versatility in solving various geometric problems efficiently. However, a potential disadvantage is the complexity of setting up proportions correctly, which may require careful attention to detail.
Best practices for implementing unit 6 similar triangles
- Label corresponding sides and angles clearly
- Double-check your proportions before solving for unknown variables
- Practice with a variety of examples to develop a strong grasp of the concept
Real-life examples of unit 6 similar triangles
- Scaling down a blueprint of a building to create a model
- Determining the height of a tree using shadows and trigonometry
- Estimating the distance between two landmarks using similar triangles
Challenges and solutions for unit 6 similar triangles
Challenge: Identifying similar triangles in complex geometric figures Solution: Break down the figure into smaller triangles to identify similarities more easily
Questions related to unit 6 similar triangles
- How do you determine if two triangles are similar?
- What is the significance of the scale factor in similar triangles?
- Can you have two similar triangles with all sides equal?
Tips and tricks for unit 6 similar triangles
- Remember that corresponding angles of similar triangles are congruent
- Use the properties of ratios and proportions to solve for unknown variables efficiently
Conclusion: Unlocking the beauty and complexity of unit 6 similar triangles opens up a world of possibilities in geometry and real-world applications. By mastering this concept, you'll gain a deeper understanding of proportions, ratios, and problem-solving techniques. So, roll up your sleeves, sharpen your pencils, and embark on an exciting journey through the world of unit 6 similar triangles.
Cracking the code average size of a master bathroom sq ft and why it matters
Two braid man bun a modern take on timeless style
Reigning country kings who makes the cut for top 10 male country singers today
