Ontdek de kracht van sinus, cosinus en tangens: Onmisbare hulpmiddelen in de wiskunde
Stel je voor: je bent aan het wandelen in een dicht bos en ineens kom je bij een rivier. Aan de overkant zie je een prachtige waterval. Je wilt de afstand tot de waterval bepalen, maar de rivier is te breed om over te steken. Hoe ga je te werk?
Dit is een van de vele situaties waarin trigonometrie, en in het bijzonder de sinus-, cosinus- en tangensregels (sin cos tan), van onschatbare waarde zijn. Deze wiskundige gereedschappen stellen ons in staat om hoeken en zijden van driehoeken te berekenen, wat ons opent voor een wereld van toepassingen in de echte wereld.
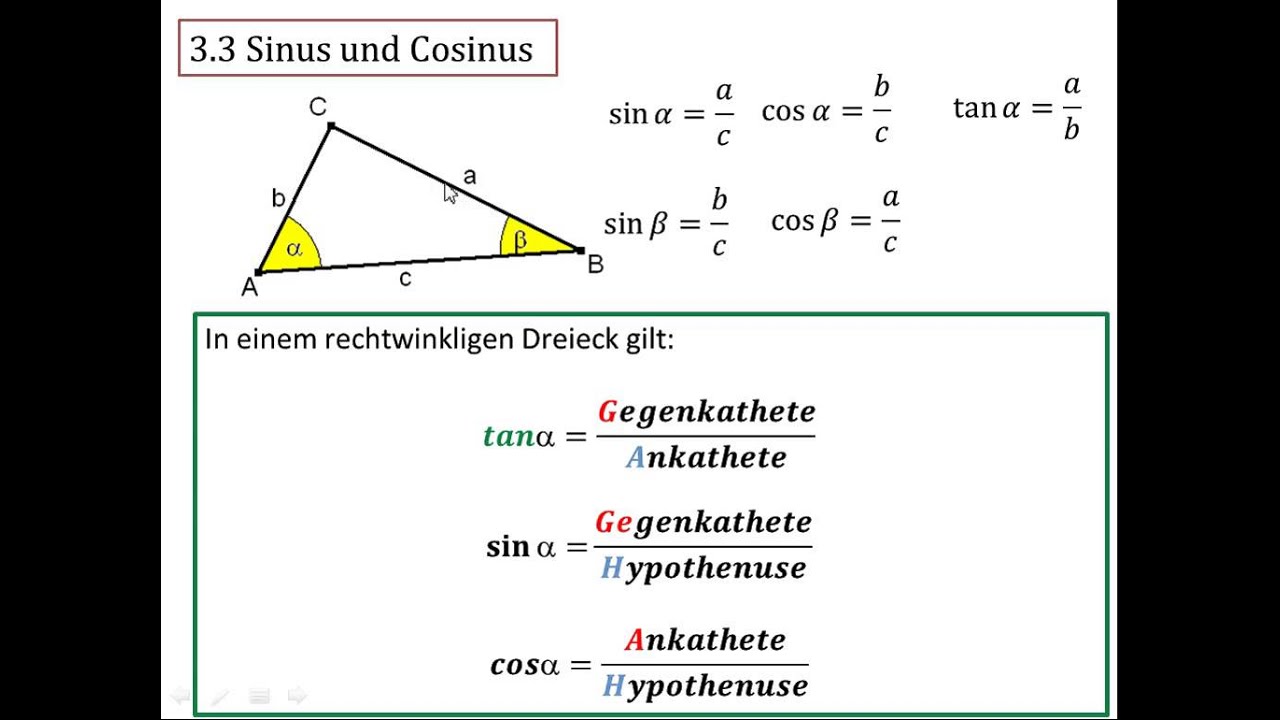
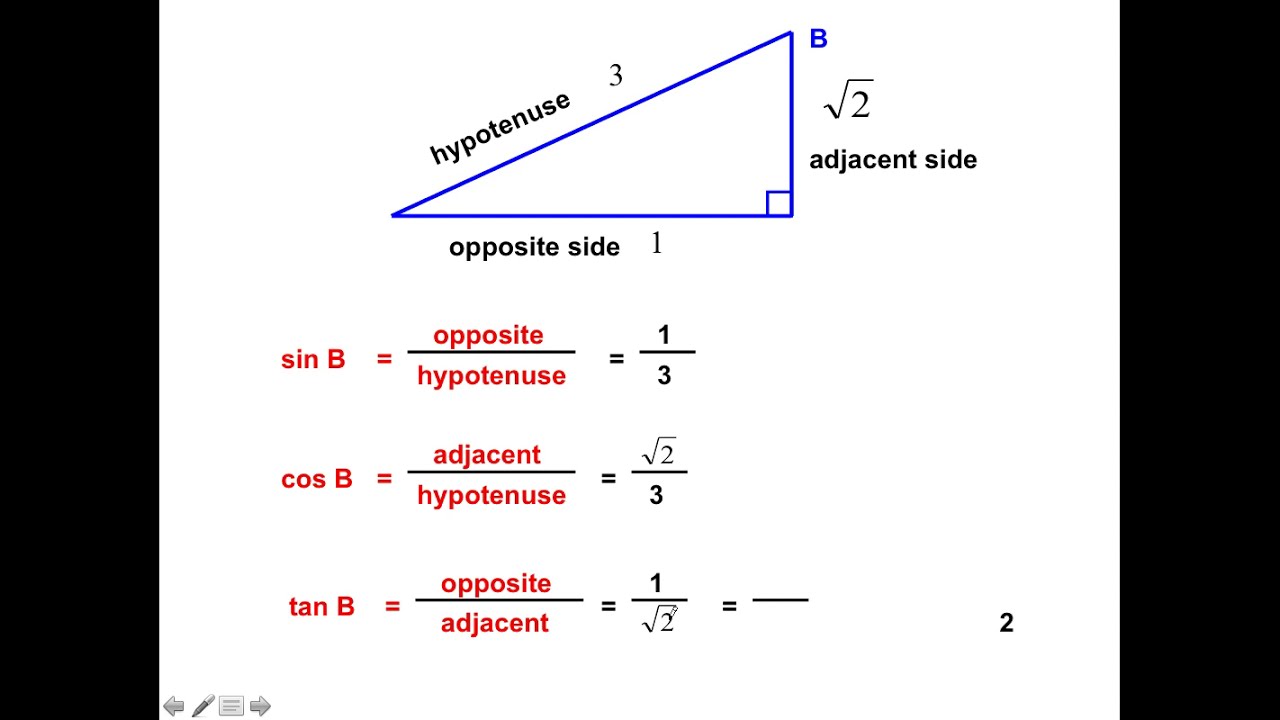
Sinus, cosinus en tangens, vaak afgekort als sin, cos en tan, zijn trigonometrische functies die de verhouding tussen de hoeken en zijden van een rechthoekige driehoek beschrijven. In de context van een rechthoekige driehoek met een bepaalde hoek θ, wordt de sinus van θ gedefinieerd als de verhouding tussen de lengte van de overstaande zijde en de lengte van de schuine zijde. Cosinus is de verhouding tussen de lengte van de aanliggende zijde en de lengte van de schuine zijde. Tangens is de verhouding tussen de lengte van de overstaande zijde en de lengte van de aanliggende zijde.
De geschiedenis van trigonometrie gaat terug tot de oude beschavingen van Egypte en Babylonië, waar deze wiskundige concepten werden gebruikt voor landmeting, astronomie en navigatie. De Griekse astronoom Hipparchus van Nicaea wordt beschouwd als de vader van de trigonometrie, omdat hij de eerste trigonometrische tabel ontwikkelde.
Tegenwoordig spelen sin, cos en tan een fundamentele rol in verschillende vakgebieden, waaronder natuurkunde, techniek, architectuur, computergraphics en meer. Ze worden gebruikt om alles te berekenen, van de baan van een projectiel tot de constructie van bruggen en gebouwen.
Voordelen van Sin Cos Tan
De voordelen van het begrijpen en toepassen van sinus, cosinus en tangens zijn talrijk. Hieronder lichten we er drie uit:
- Problemen met driehoeken oplossen: Met behulp van de sin cos tan regels kun je onbekende zijden en hoeken van rechthoekige driehoeken berekenen. Dit is met name handig in de bouwkunde, landmeetkunde en navigatie.
- Modelleren van periodieke verschijnselen: Veel verschijnselen in de natuur, zoals golven, trillingen en geluidsgolven, vertonen een periodiek gedrag. Sin en cos functies zijn ideaal om deze verschijnselen te modelleren en te analyseren.
- Vergemakkelijken van complexe berekeningen: In geavanceerde wiskundige en natuurkundige toepassingen kunnen sin, cos en tan gebruikt worden om complexe vergelijkingen te vereenvoudigen en op te lossen.
Praktische toepassingen
De toepassingen van sin, cos en tan in de praktijk zijn legio. Hier zijn vijf concrete voorbeelden:
- Navigatie: Een piloot kan sin, cos en tan gebruiken om de koers van een vliegtuig te bepalen, rekening houdend met de windrichting en -snelheid.
- Bouwkunde: Ingenieurs gebruiken deze trigonometrische functies om de belasting en spanning in bruggen, gebouwen en andere constructies te berekenen.
- Computergraphics: Sin, cos en tan worden gebruikt om 3D-objecten te roteren, te verplaatsen en te schalen in computerspellen en animaties.
- Muziek: De golven die muziek produceren, kunnen worden weergegeven met behulp van sinus- en cosinusfuncties, wat van cruciaal belang is voor het ontwerp van muziekinstrumenten en geluidsapparatuur.
- Medische beeldvorming: Technieken zoals echografie en CT-scans gebruiken trigonometrische functies om beelden van interne organen en weefsels te reconstrueren.
Veelgestelde vragen
Hier zijn acht veelgestelde vragen met antwoorden over sin, cos en tan:
- Wat is het verschil tussen sin, cos en tan?
Sin, cos en tan zijn trigonometrische functies die de verhouding tussen de zijden van een rechthoekige driehoek beschrijven. Sin is de overstaande zijde gedeeld door de schuine zijde, cos is de aanliggende zijde gedeeld door de schuine zijde en tan is de overstaande zijde gedeeld door de aanliggende zijde.
- Waarvoor worden sin, cos en tan gebruikt?
Sin, cos en tan worden gebruikt om onbekende zijden en hoeken van rechthoekige driehoeken te berekenen. Ze worden toegepast in verschillende vakgebieden, zoals navigatie, bouwkunde, computergraphics en meer.
- Wat is de eenheidscirkel in trigonometrie?
De eenheidscirkel is een cirkel met een straal van 1, gebruikt om trigonometrische waarden te visualiseren en te begrijpen.
- Wat is de relatie tussen sin, cos en tan?
De drie functies zijn met elkaar verbonden door de identiteit: tan θ = sin θ / cos θ.
- Wat zijn de inverse trigonometrische functies?
De inverse trigonometrische functies, aangeduid als arcsin, arccos en arctan, worden gebruikt om de hoek te vinden die overeenkomt met een gegeven trigonometrische waarde.
- Hoe kan ik sin, cos en tan berekenen zonder rekenmachine?
Je kunt trigonometrische tabellen of speciale driehoeken (30-60-90 en 45-45-90) gebruiken om de waarden te bepalen.
- Wat zijn enkele tips voor het onthouden van sin, cos en tan?
Gebruik ezelsbruggetjes zoals "SOH CAH TOA" (Sin = Overstaande / Schuine, Cos = Aanliggende / Schuine, Tan = Overstaande / Aanliggende).
- Waar kan ik meer leren over sin, cos en tan?
Er zijn veel online bronnen, leerboeken en video's beschikbaar om je kennis van trigonometrie te verdiepen. Websites zoals Khan Academy en MathPapa bieden gratis lessen en oefeningen.
Conclusie
Sinus, cosinus en tangens zijn onmisbare hulpmiddelen in de wiskunde en vele andere wetenschappen. Van het oplossen van eenvoudige driehoeken tot het modelleren van complexe verschijnselen, deze trigonometrische functies stellen ons in staat om de wereld om ons heen beter te begrijpen en te manipuleren. Door hun brede scala aan toepassingen zijn sin, cos en tan essentiële concepten voor iedereen die geïnteresseerd is in wetenschap, technologie, engineering of wiskunde. Investeer tijd in het leren en begrijpen van deze fundamentele trigonometrische functies en ontdek een wereld van mogelijkheden.
Door te experimenteren met verschillende toepassingen van sin, cos en tan, kun je je vaardigheden verder ontwikkelen en hun kracht in verschillende contexten benutten. Vergeet niet dat oefening kunst baart! Blijf oefenen met problemen en pas je kennis toe in praktische situaties om je begrip van deze krachtige wiskundige tools te versterken.
Ontdek wat jou bijzonder maakt
Tram 4 den haag jouw complete gids voor de route
Zelfreinigende kattenbak robot 4 de ultieme gids