Risolvere Sistemi di Equazioni: La Guida Completa con il Metodo Grafico
Immaginate di dover organizzare un evento e di dover scegliere tra due catering che offrono pacchetti diversi. Come potreste determinare quale opzione si adatta meglio alle vostre esigenze e al vostro budget? In matematica, ci troviamo spesso di fronte a situazioni in cui abbiamo bisogno di trovare la soluzione ottimale che soddisfi più condizioni contemporaneamente. Questo è dove entrano in gioco i sistemi di equazioni, e il metodo grafico ci offre uno strumento potente e intuitivo per risolverli.
Ma cosa sono esattamente i sistemi di equazioni? In parole semplici, un sistema di equazioni è un insieme di due o più equazioni che devono essere soddisfatte contemporaneamente. Ogni equazione rappresenta una condizione o una relazione tra le variabili in gioco. Risolvere un sistema di equazioni significa trovare i valori delle variabili che rendono vere tutte le equazioni del sistema.
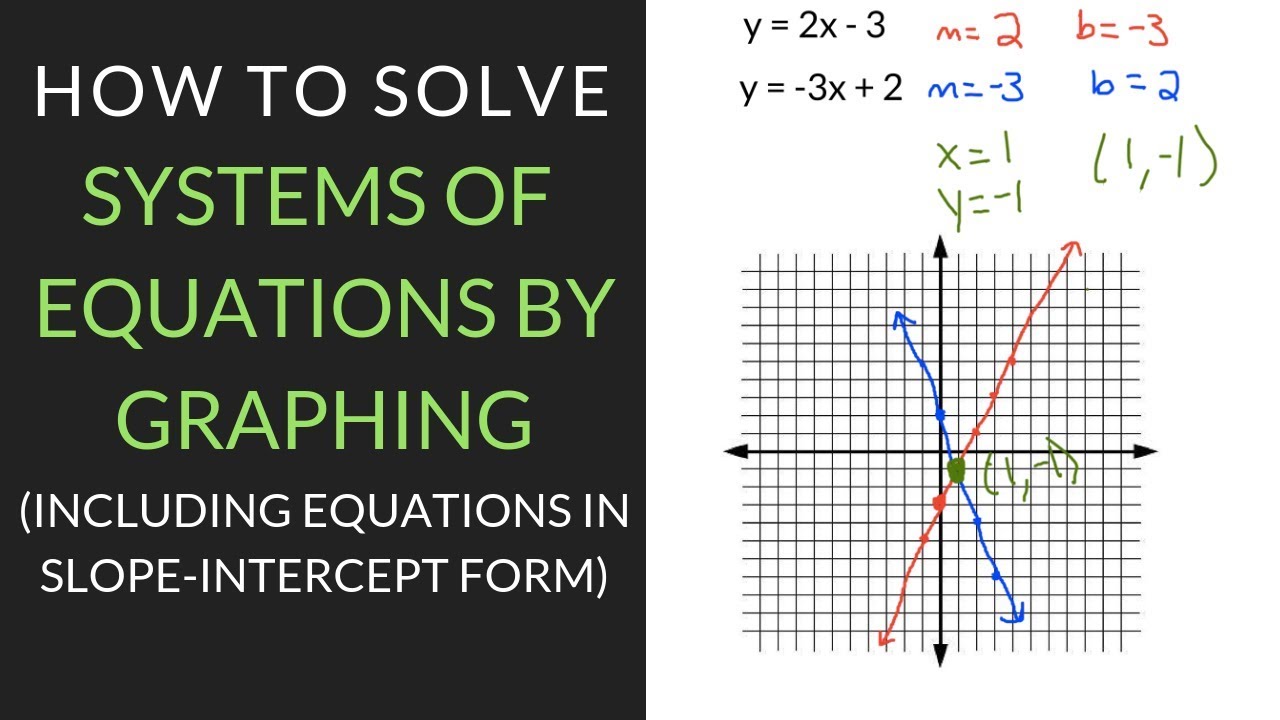
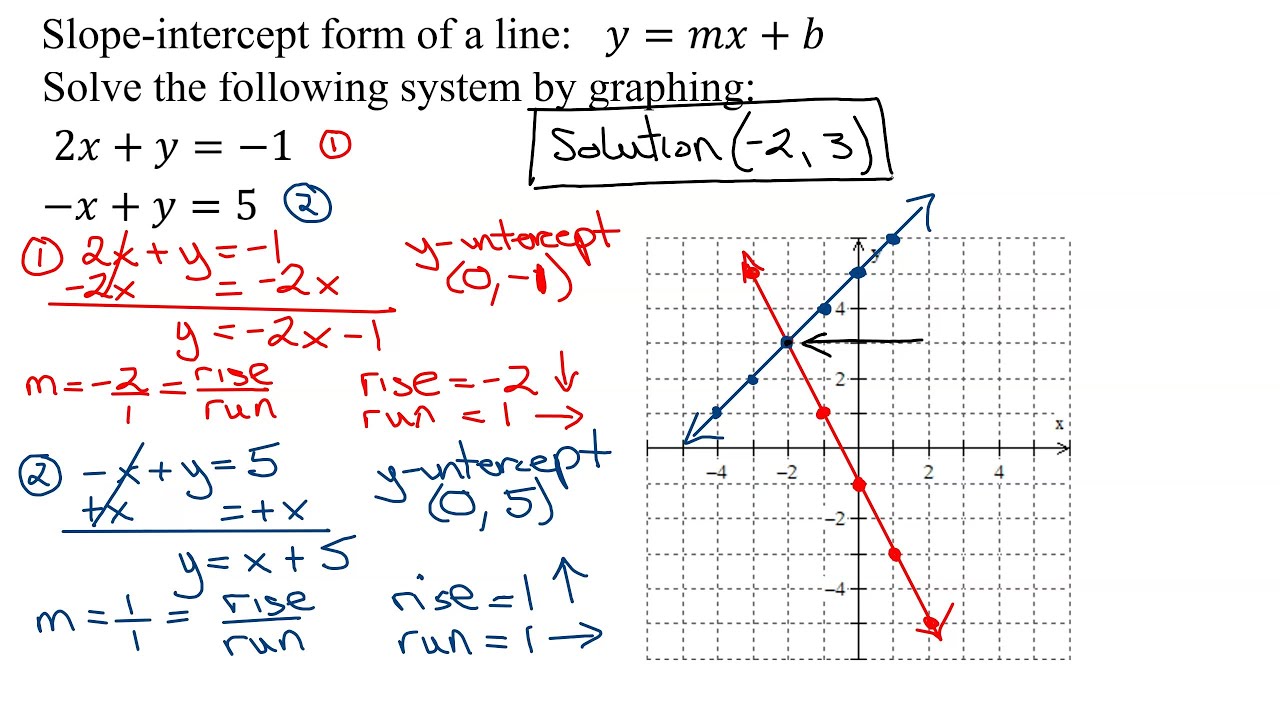
Il metodo grafico per la risoluzione di sistemi di equazioni si basa sulla rappresentazione grafica delle equazioni su un piano cartesiano. Ogni equazione viene rappresentata da una retta, e la soluzione del sistema corrisponde al punto (o ai punti) di intersezione tra le rette. Questo approccio visivo ci permette di "vedere" la soluzione e di avere un'idea immediata del comportamento del sistema.
Il metodo grafico trova le sue radici nell'antica Grecia, dove geometri e matematici come Euclide e Apollonio svilupparono i primi concetti di geometria analitica, gettando le basi per la rappresentazione grafica di equazioni. Nel corso dei secoli, il metodo grafico ha assunto un ruolo centrale in diversi campi della matematica, della fisica, dell'ingegneria e dell'economia, offrendo uno strumento versatile per la modellizzazione e la risoluzione di problemi complessi.
Nonostante la sua potenza e intuitività, il metodo grafico presenta alcune limitazioni. La precisione della soluzione dipende dalla precisione del grafico, e può essere difficile ottenere soluzioni precise per sistemi con equazioni complesse o con un numero elevato di variabili. Inoltre, il metodo grafico non è sempre il più efficiente, soprattutto quando si ha a che fare con sistemi di grandi dimensioni.
Vantaggi e Svantaggi del Metodo Grafico
| Vantaggi | Svantaggi |
|---|---|
| Intuitivo e facile da visualizzare | Precisione limitata dalla precisione del grafico |
| Utile per comprendere il comportamento del sistema | Difficile da applicare a sistemi con molte variabili |
| Offre una soluzione approssimativa anche quando le soluzioni esatte sono difficili da calcolare | Non sempre il metodo più efficiente |
Oltre ai vantaggi e agli svantaggi elencati nella tabella, è importante sottolineare che il metodo grafico può essere particolarmente utile come strumento didattico per introdurre i concetti di sistemi di equazioni e per sviluppare l'intuizione geometrica degli studenti.
Per concludere, il metodo grafico per la risoluzione di sistemi di equazioni rappresenta un approccio potente e intuitivo che ci permette di "vedere" la soluzione e di comprendere meglio il comportamento del sistema. Nonostante le sue limitazioni, il metodo grafico rimane uno strumento fondamentale in diversi campi della matematica e delle scienze applicate, offrendo una soluzione visuale ed elegante a problemi che coinvolgono la ricerca di un equilibrio tra diverse condizioni.
Costruire un cilindro con la carta la guida completa
Libera la tua immaginazione una guida ai testi di scrittura creativa
Somos lo que vemos como impacta nuestra mirada en la vida