Démêler les mystères de la droite d'ajustement : Un guide pour comprendre et l'appliquer
Dans un monde inondé de données, la capacité à donner un sens aux chiffres est devenue plus précieuse que jamais. Que ce soit pour prédire les tendances du marché, comprendre l'impact d'une campagne marketing ou analyser des résultats scientifiques, la recherche de relations significatives au sein d'un ensemble de données est primordiale. C'est là qu'intervient la notion de droite d'ajustement, un outil statistique puissant qui nous permet de visualiser et de modéliser des relations entre différentes variables. Mais comment s'y prendre pour calculer cette fameuse droite d'ajustement et, surtout, comment l'interpréter ?
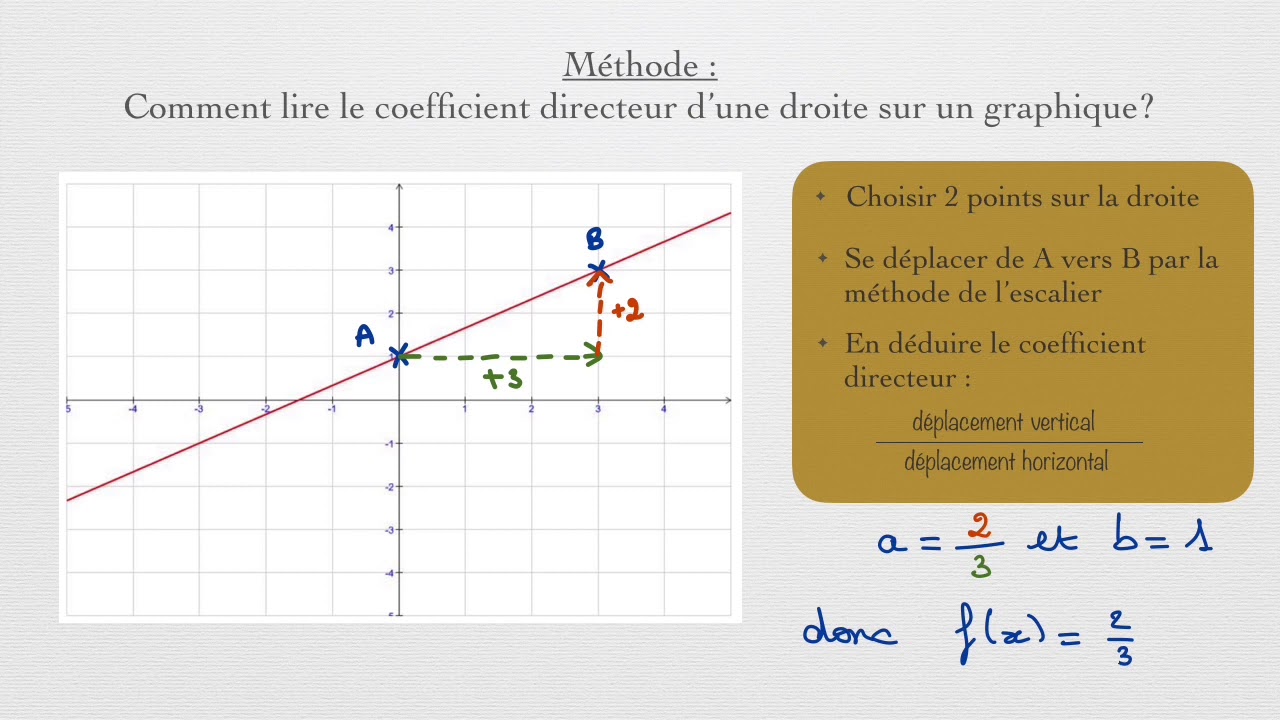
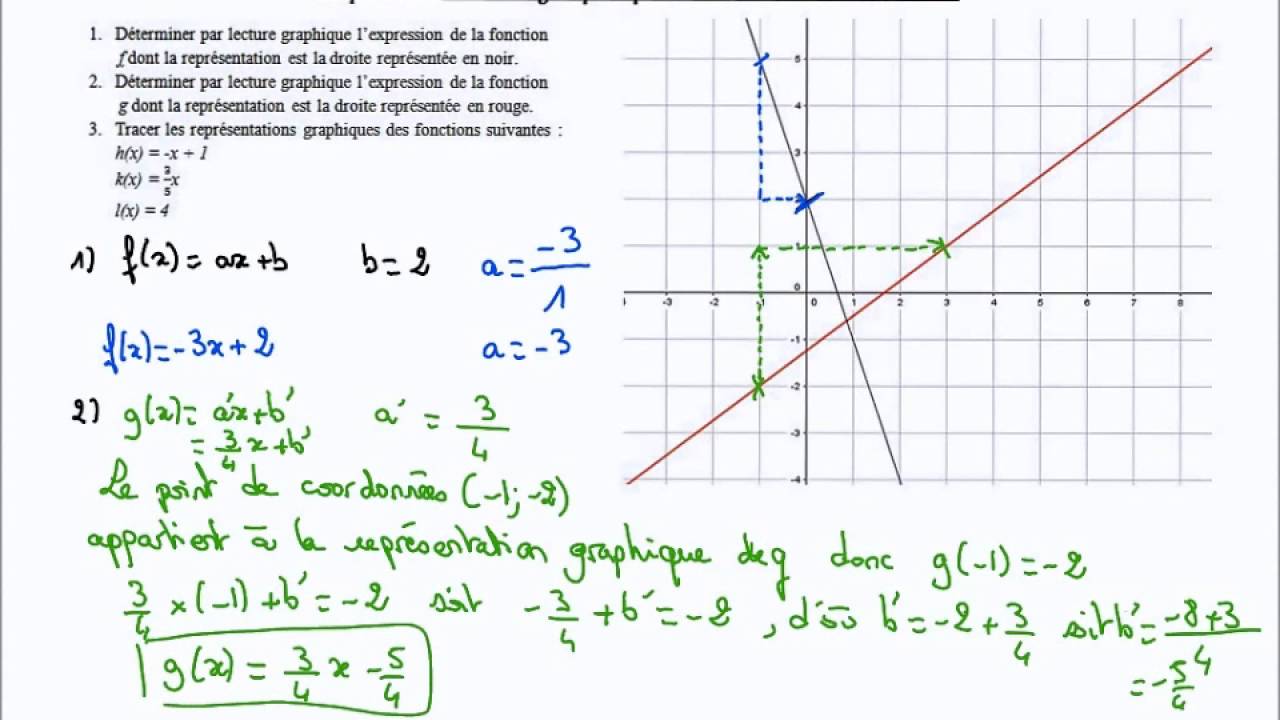
L'histoire de la droite d'ajustement remonte aux travaux pionniers de Legendre et Gauss au début du XIXe siècle. Face à des problèmes d'astronomie et de géodésie, ces mathématiciens ont développé la méthode des moindres carrés, qui allait révolutionner l'analyse des données. Le principe est simple : trouver la droite qui minimise la somme des carrés des distances entre chaque point de données et la droite elle-même. Cette droite, appelée "droite de régression linéaire" ou "droite d'ajustement", représente la meilleure approximation linéaire de la relation entre les variables étudiées.
L'importance de la droite d'ajustement réside dans sa capacité à nous aider à comprendre et à prédire des phénomènes. En effet, une fois la droite calculée, il est possible d'estimer la valeur d'une variable en fonction d'une autre, et ce même en dehors des données initiales. Par exemple, si l'on étudie la relation entre le nombre d'heures travaillées et le salaire perçu, la droite d'ajustement nous permettra d'estimer le salaire d'une personne en fonction de son nombre d'heures de travail, même si cette combinaison précise n'est pas présente dans les données originales.
Cependant, il est crucial de garder à l'esprit que la droite d'ajustement n'est qu'une approximation de la réalité. La relation entre deux variables peut être influencée par de nombreux facteurs, et il est rare qu'elle soit parfaitement linéaire. Il est donc important de ne pas tirer de conclusions hâtives à partir de la seule observation de la droite d'ajustement et de toujours prendre en compte le contexte et les limites de l'analyse.
Un autre point important à souligner est la différence entre corrélation et causalité. Le fait que deux variables soient corrélées, c'est-à-dire que la droite d'ajustement montre une relation claire, ne signifie pas nécessairement qu'il existe un lien de cause à effet entre elles. Il est possible que d'autres variables cachées influencent les deux variables étudiées, créant ainsi une corrélation fallacieuse. Par exemple, on pourrait observer une corrélation positive entre la vente de glaces et le nombre de coups de soleil. Cela ne signifie pas que manger des glaces provoque des coups de soleil, mais plutôt que ces deux phénomènes sont influencés par une variable commune : la chaleur estivale.
Malgré ces mises en garde, la droite d'ajustement reste un outil précieux pour l'analyse de données. En comprenant ses forces et ses limites, nous pouvons l'utiliser avec discernement pour éclairer nos décisions et mieux appréhender le monde qui nous entoure.
Festival de cannes le guide complet des paillettes au tapis rouge
Decryptage de la feuille de route la strategie dentreprise et ses enjeux
Les morceaux incontournables de ginger bakers air force un voyage musical explosif
