Die Heisenberg-Gruppe und K-Theorie: Ein faszinierendes Duo
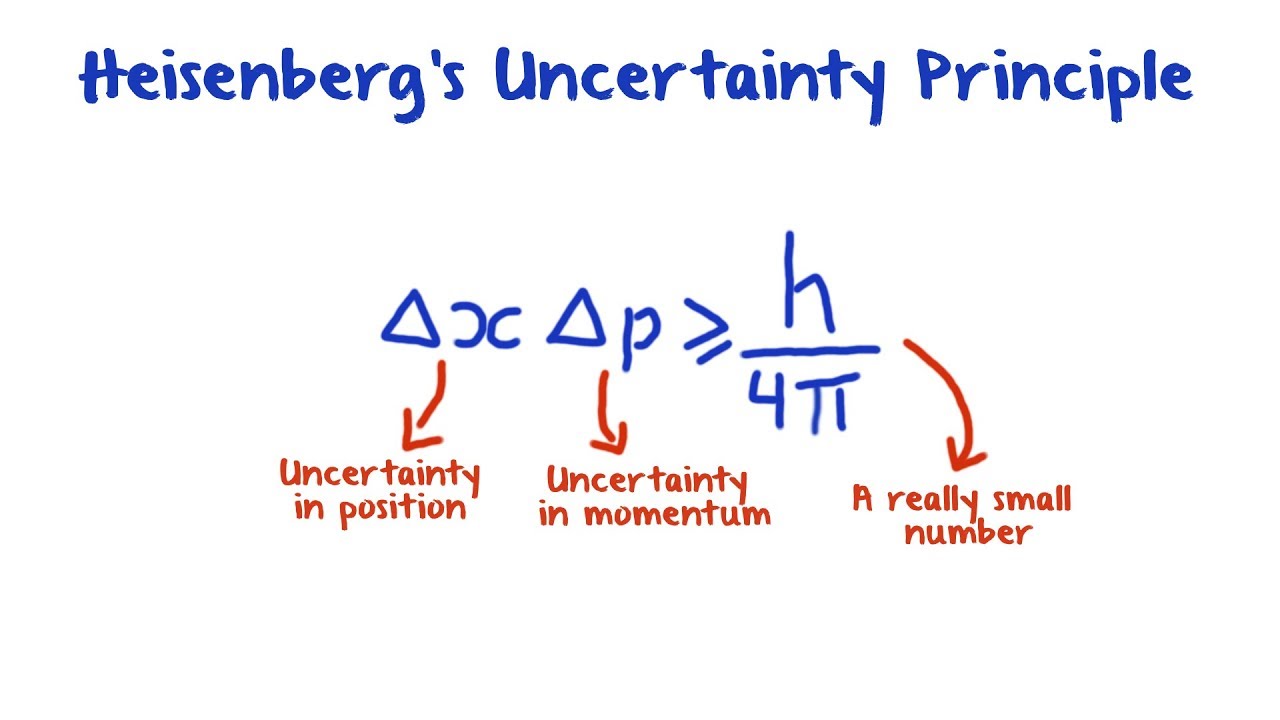
Stellen Sie sich vor, Sie könnten die Position und den Impuls eines Elektrons gleichzeitig bestimmen. Klingt unmöglich? Die Heisenbergsche Unschärferelation besagt genau das – eine fundamentale Grenze unserer Fähigkeit, die Welt der Quanten zu messen. Doch was hat diese fundamentale Aussage der Physik mit der abstrakten Welt der Mathematik, genauer gesagt der K-Theorie, zu tun? Hier betreten wir die faszinierende Schnittstelle zwischen der Heisenberg-Gruppe und der K-Theorie.
Die Heisenberg-Gruppe, benannt nach dem Physiker Werner Heisenberg, ist eine mathematische Struktur, die in der Quantenmechanik eine zentrale Rolle spielt. Sie beschreibt die Beziehung zwischen Position, Impuls und Drehimpuls eines Teilchens und verdeutlicht die Grenzen der gleichzeitigen Messbarkeit dieser Größen. Die K-Theorie hingegen, ein Zweig der algebraischen Topologie, mag auf den ersten Blick weit entfernt von der Quantenwelt erscheinen. Sie befasst sich mit der Klassifizierung von Vektorräumen und ihren Transformationen und liefert überraschende Einblicke in die Struktur von Räumen und Funktionen.
Die Verbindung zwischen diesen beiden scheinbar unterschiedlichen Gebieten liegt in der Sprache der Mathematik. Die Heisenberg-Gruppe, obwohl aus der Physik geboren, kann als mathematisches Objekt betrachtet werden, das mit den Werkzeugen der K-Theorie analysiert werden kann. Tatsächlich stellt die K-Theorie eine elegante und mächtige Methode dar, um die Eigenschaften der Heisenberg-Gruppe zu untersuchen. Durch die Anwendung von K-theoretischen Konzepten können wir tiefere Einblicke in die Struktur und die Darstellungstheorie der Heisenberg-Gruppe gewinnen und so auch unser Verständnis der Quantenmechanik verfeinern.
Die Untersuchung der Heisenberg-Gruppe und ihrer Verbindung zur K-Theorie ist nicht nur von akademischem Interesse. Vielmehr eröffnen sich durch diese Verbindung neue Perspektiven auf fundamentale Fragen der Mathematik und Physik. Zum Beispiel können K-theoretische Methoden helfen, die Eigenschaften von Quantenfeldtheorien besser zu verstehen und neue mathematische Modelle für die Beschreibung der Quantenwelt zu entwickeln. Die Erforschung der Schnittstelle zwischen Heisenberg-Gruppe und K-Theorie birgt daher ein enormes Potenzial für die Weiterentwicklung unseres Wissens und die Entdeckung neuer Zusammenhänge zwischen den fundamentalen Bausteinen der Natur.
Die Heisenberg-Gruppe und die K-Theorie mögen auf den ersten Blick abstrakte mathematische Konzepte sein, doch ihre Verbindung offenbart eine faszinierende Brücke zwischen der Welt der Quanten und der Welt der Mathematik. Diese Brücke zu erkunden verspricht nicht nur ein tieferes Verständnis der fundamentalen Gesetze der Natur, sondern auch die Entdeckung neuer mathematischer Strukturen und Zusammenhänge, die unser Bild von der Welt bereichern. Es bleibt spannend zu beobachten, welche weiteren Geheimnisse die Heisenberg-Gruppe und die K-Theorie in Zukunft für uns bereithalten.
Blumen in vasen bilder zeitlose schonheit auf leinwand und foto
Krieger mit speer ikone der geschichte und ihre bedeutung
Mathe power fur die 7 klasse ubungsblatter zum download