Brüche verstehen gleichwertige Brüche für Kinder erklärt
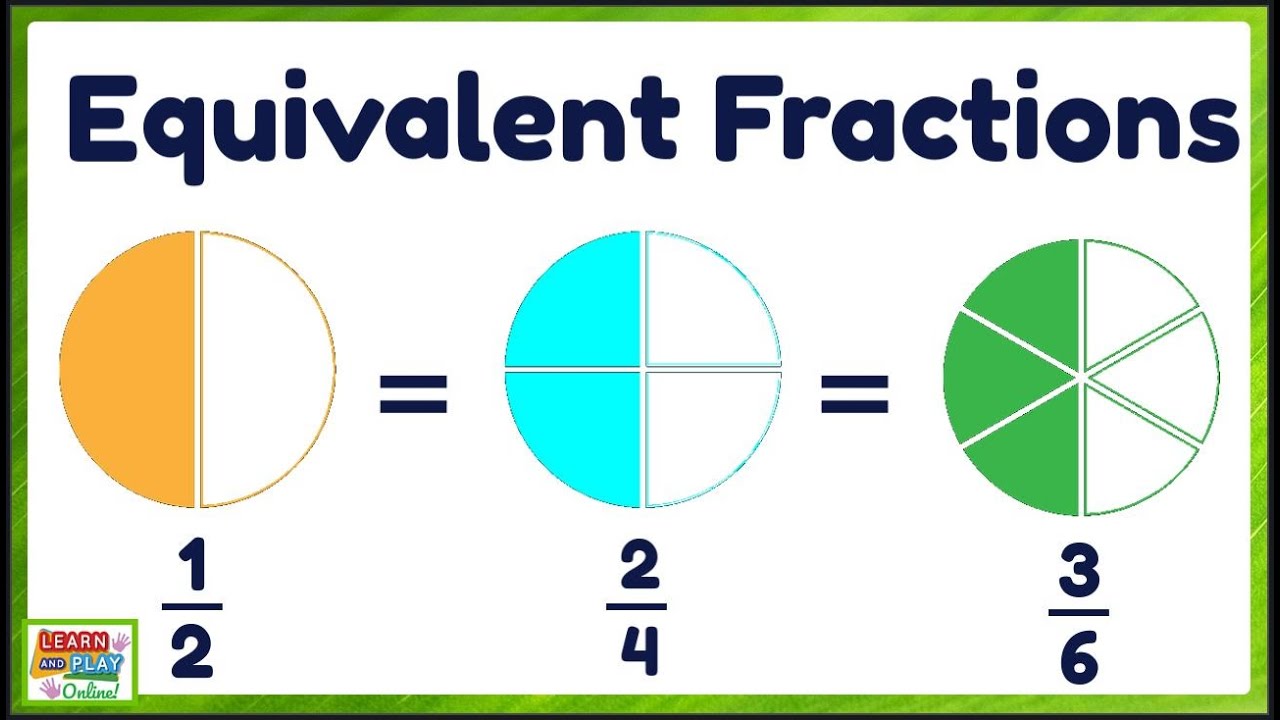
Was ist ein halbes Stück Kuchen und wie kann man es auf verschiedene Weisen darstellen? Stell dir vor, du hast einen Kuchen und teilst ihn in zwei gleiche Stücke. Du nimmst ein Stück. Das ist die Hälfte, oder auch ein Halb, geschrieben als 1/2. Aber was passiert, wenn du den gleichen Kuchen in vier gleiche Stücke teilst und zwei davon nimmst? Du hast immer noch die gleiche Menge Kuchen! Das ist die Idee hinter gleichwertigen Brüchen.
Gleichwertige Brüche, oder auch gleichnamige Brüche, sind Brüche, die den gleichen Wert darstellen, obwohl sie unterschiedlich aussehen. Wie im Kuchenbeispiel, 1/2 und 2/4 sind gleichwertig, weil sie die gleiche Menge Kuchen repräsentieren. Das Verstehen von gleichwertigen Brüchen ist ein grundlegendes Konzept im Bruchrechnen und hilft Kindern, Brüche zu vergleichen, zu addieren und zu subtrahieren.
Das Konzept von Brüchen und gleichwertigen Brüchen ist schon seit der Antike bekannt. Die Ägypter verwendeten bereits Brüche, allerdings mit einer anderen Schreibweise als heute. Das heutige System mit Zähler und Nenner entwickelte sich über Jahrhunderte und wurde durch Mathematiker wie Al-Chwarizmi weiterentwickelt. Die Bedeutung von gleichwertigen Brüchen liegt darin, dass sie das Rechnen mit Brüchen vereinfachen. Man kann Brüche auf einen gemeinsamen Nenner bringen und sie dann leichter addieren oder subtrahieren.
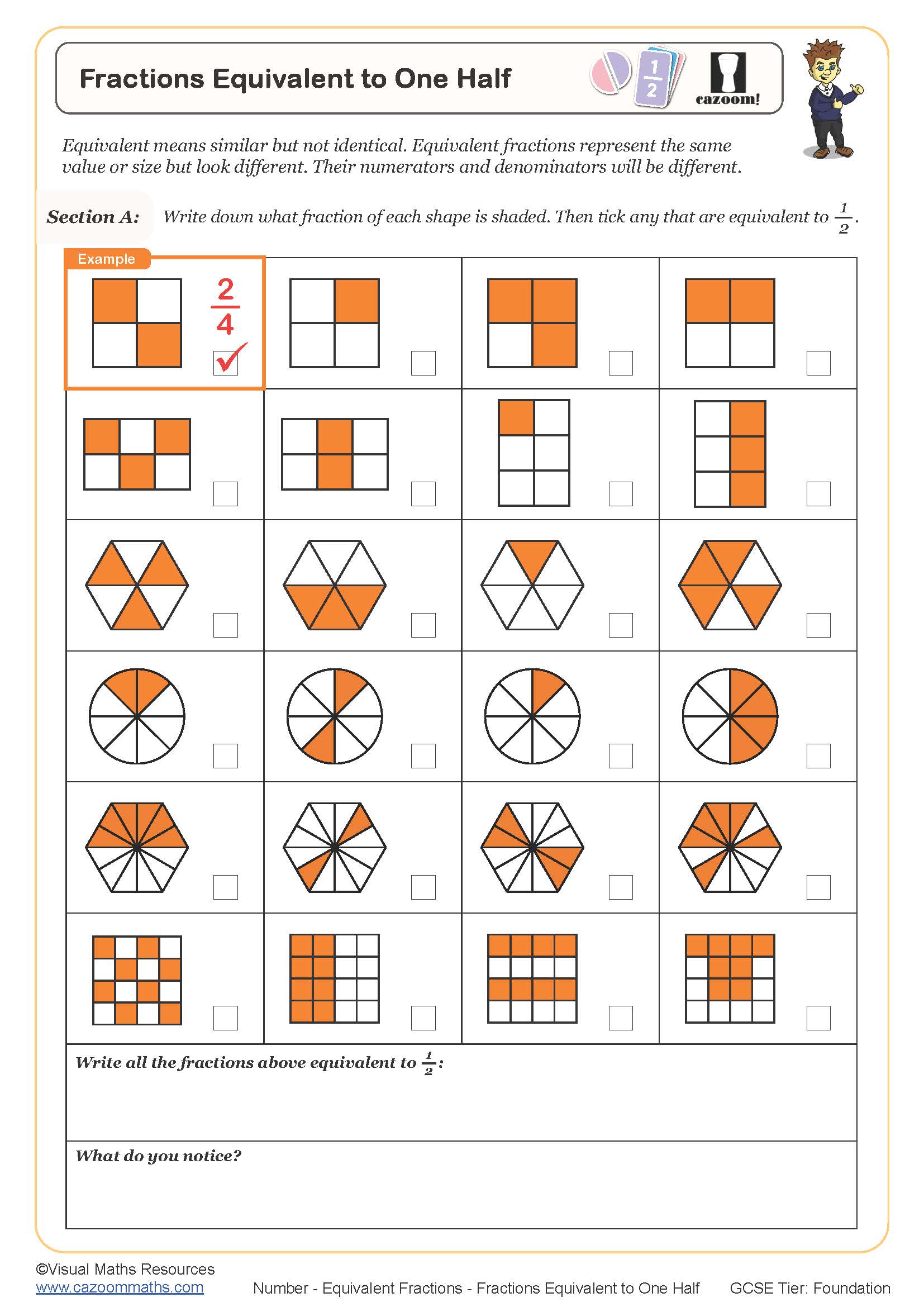
Ein häufiges Problem beim Verständnis von gleichwertigen Brüchen ist, dass Kinder sich auf die Zahlen konzentrieren und nicht auf den Wert, den der Bruch darstellt. Sie sehen 1/2 und 2/4 als unterschiedliche Mengen an, obwohl sie gleichwertig sind. Es ist wichtig, den Kindern den Zusammenhang zwischen dem Bruch und einer visuellen Darstellung, wie dem Kuchenbeispiel, zu verdeutlichen.
Eine einfache Definition von gleichwertigen Brüchen für Kinder ist: Brüche, die die gleiche Größe oder den gleichen Anteil von einem Ganzen darstellen, obwohl sie unterschiedlich geschrieben sind. Um gleichwertige Brüche zu finden, kann man den Zähler und den Nenner mit der gleichen Zahl multiplizieren oder dividieren. Zum Beispiel: 1/2 multipliziert mit 2 im Zähler und Nenner ergibt 2/4. Umgekehrt, 2/4 dividiert durch 2 im Zähler und Nenner ergibt 1/2.
Ein weiteres Beispiel: 3/5 ist gleichwertig mit 6/10, 9/15 und 12/20, da jeweils Zähler und Nenner mit derselben Zahl (2, 3 und 4) multipliziert wurden.
Vorteile von gleichwertigen Brüchen: 1. Vereinfachtes Vergleichen von Brüchen, 2. Einfacheres Addieren und Subtrahieren von Brüchen, 3. Besseres Verständnis von Anteilen und Verhältnissen.
Aktionsplan: 1. Visuelle Darstellungen verwenden (z.B. Kuchen, Kreise, Rechtecke), 2. Mit kleinen Zahlen beginnen und schrittweise steigern, 3. Spiele und Übungen verwenden, um das Verständnis zu festigen.
Häufig gestellte Fragen: 1. Was ist ein Bruch? 2. Was ist ein Zähler? 3. Was ist ein Nenner? 4. Wie finde ich gleichwertige Brüche? 5. Warum sind gleichwertige Brüche wichtig? 6. Wie kann ich Brüche vergleichen? 7. Wie addiere ich Brüche? 8. Wie subtrahiere ich Brüche?
Tipps und Tricks: Verwenden Sie Alltagsgegenstände wie Pizza oder Schokolade, um gleichwertige Brüche zu veranschaulichen. Spielen Sie Spiele mit Bruchkärtchen. Üben Sie regelmäßig mit verschiedenen Aufgaben.
Zusammenfassend lässt sich sagen, dass das Verständnis von gleichwertigen Brüchen ein wichtiger Baustein im Bruchrechnen ist. Durch die Verwendung von visuellen Hilfsmitteln, spielerischen Übungen und der Verbindung zu alltäglichen Situationen können Kinder dieses Konzept leichter begreifen. Die Fähigkeit, gleichwertige Brüche zu erkennen und zu bilden, erleichtert das Vergleichen, Addieren und Subtrahieren von Brüchen und fördert ein tieferes Verständnis von Anteilen und Verhältnissen. Ermutigen Sie Kinder, mit Brüchen zu experimentieren und verschiedene Darstellungen zu erkunden. Ein solides Verständnis von gleichwertigen Brüchen legt den Grundstein für den späteren Erfolg in der Mathematik und im Umgang mit alltäglichen Problemstellungen, die Brüche beinhalten, sei es beim Backen, beim Teilen von Ressourcen oder beim Verstehen von Statistiken.
Personlicher kontakt bei kaffee und kuchen
Sich selbst im weg stehen verstehen und uberwinden
Stephanie graefin bruges von pfuel